حقائق سريعة
- ميكانيك لاغرانج هي إعادة صياغة للميكانيك الكلاسيكية (ميكانيك نيوتن)، قام لاغرانج عام 1788. في الميكانيك اللاغرانجية: يُحسب مسار جسم ما من خلال حل معادلة لاغرانج بأحد شكليها اللذين يختلفان عن بعضهما بكيفية التعامل مع التقييدات الفيزيائية ( التقييدات في الفيزياء هي أمور لا يمكن للنظام الفيزيائي تجاوزها).
- عام 1787، عندما كان عمره 51 عامًا، انتقل من برلين إلى باريس وأصبح عضوًا في الأكاديمية الفرنسية للعلوم. وبقي في فرنسا حتى نهاية حياته. كان له دور فعال في عملية التقسيم العشري في فرنسا الثورية، وأصبح أول أستاذ للتحليل في مدرسة البوليتكنيك عند افتتاحها في عام 1794، وكان عضوًا مؤسسًا في مكتب خطوط الطول، وأصبح عضوًا في مجلس الشيوخ في عام 1799.
- كان من المفترض أن يحافظ والده، الذي كان مسؤولاً عن الصندوق العسكري للملك وكان أمين صندوق مكتب الأشغال العامة والتحصينات في تورينو، على وضع اجتماعي جيد وثروة، ولكن قبل أن يكبر ابنه كان قد فقد معظم ممتلكاته في المضاربات.
- اخترع لاغرانج طريقة حل المعادلات التفاضلية المعروفة باسم اختلاف المعلمات.
معلومات نادرة
- لماذا غير اسمه؟ عندما ولد، كانت تورينو قد تحولت بالفعل إلى عاصمة سردينيا. قام لاغرانج فيما بعد بتغيير اسمه ليبدو فرنسيًا أكثر عندما أصبح مواطنًا متجنسًا في بلده.
- ما هي نقطة لاغرانج؟
نقاط لاغرانج هي مواضع في الفضاء حيث تميل الأجسام المرسلة إلى البقاء في مكانها. عند نقاط لاغرانج، فإن قوة الجاذبية لكتلتين كبيرتين تساوي بدقة قوة الجذب المركزي اللازمة لجسم صغير ليتحرك معهم. يمكن للمركبات الفضائية استخدام هذه النقاط في الفضاء لتقليل استهلاك الوقود اللازم للبقاء في موضعها.
نقاط لاغرانج هي مواقع في الفضاء حيث تنتج قوى الجاذبية لنظام مكون من جسمين مثل الشمس والأرض مناطق محسنة من الجذب والتنافر. يمكن استخدامها بواسطة المركبات الفضائية لتقليل استهلاك الوقود اللازم للبقاء في الموقع.
تم تسمية نقاط لاغرانج على اسم عالم الرياضيات الإيطالي الفرنسي جوزيفي لويس لاغرانج.
هناك خمس نقاط خاصة حيث يمكن للكتلة الصغيرة أن تدور بنمط ثابت مع كتلتين أكبر. نقاط لاغرانج هي مواضع حيث قوة الجاذبية لكتلتين كبيرتين تساوي بدقة قوة الجذب المركزي المطلوبة لجسم صغير ليتحرك معهم. هذه المشكلة الرياضية، المعروفة باسم “مشكلة الأجسام الثلاثة العامة”، تناولها لاغرانج في بحثه الحائز على جائزة (Essai sur le Problème des Trois Corps، 1772).
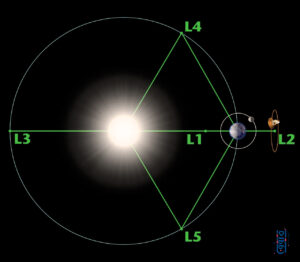
من بين نقاط لاغرانج الخمس، هناك ثلاث نقاط غير مستقرة واثنتان مستقرتان. تقع نقاط لاغرانج غير المستقرة – المسماة L1 وL2 وL3 – على طول الخط الذي يربط بين الكتلتين الكبيرتين. تشكل نقاط لاغرانج المستقرة – المسماة L4 وL5 – قمة مثلثين متساويين الأضلاع لهما كتل كبيرة في رؤوسهما. يقود L4 مدار الأرض ويتبعه L5
توفر النقطة L1 لنظام الأرض والشمس رؤية متواصلة للشمس وهي حاليًا موطن للقمر الصناعي للمرصد الشمسي والغلاف الشمسي SOHO.
كانت النقطة L2 في نظام الأرض والشمس موطنًا للمركبة الفضائية WMAP، والموطن الحالي لبلانك، والموطن المستقبلي لتلسكوب جيمس ويب الفضائي. يعتبر L2 مثاليًا لعلم الفلك لأن المركبة الفضائية قريبة بما يكفي للتواصل بسهولة مع الأرض، ويمكنها إبقاء الشمس والأرض والقمر خلف المركبة الفضائية للحصول على الطاقة الشمسية و(مع التدريع المناسب) توفر رؤية واضحة للفضاء السحيق لتلسكوباتنا. النقطتان L1 وL2 غير مستقرتين على نطاق زمني يبلغ حوالي 23 يومًا، الأمر الذي يتطلب من الأقمار الصناعية التي تدور حول هذه المواقع أن تخضع لتصحيحات منتظمة للمسار والارتفاع.
ومن غير المرجح أن تجد ناسا أي فائدة للنقطة L3 لأنها تظل مخفية خلف الشمس في جميع الأوقات. كانت فكرة الكوكب المخفي موضوعًا شائعًا في كتابة الخيال العلمي.
تعد النقطتان L4 وL5 موطنًا لمدارات مستقرة طالما أن نسبة الكتلة بين الكتلتين الكبيرتين تتجاوز 24.96. يتم استيفاء هذا الشرط لكل من نظامي الأرض والشمس والأرض والقمر، وللعديد من أزواج الأجسام الأخرى في النظام الشمسي. غالبًا ما تسمى الأجسام التي تدور حول النقطتين L4 وL5 بأحصنة طروادة نسبة إلى الكويكبات الثلاثة الكبيرة أجاممنون وأخيل وهيكتور التي تدور في النقطتين L4 وL5 من نظام المشتري والشمس. (بحسب هوميروس، كان هيكتور بطل طروادة الذي قُتل على يد أخيل أثناء حصار الملك أجاممنون لطروادة). هناك المئات من كويكبات طروادة في النظام الشمسي. معظمها يدور حول كوكب المشتري، لكن البعض الآخر يدور حول المريخ. بالإضافة إلى ذلك، فإن العديد من أقمار زحل لها أقمار طروادة مرافقة.
في عام 1956، اكتشف عالم الفلك البولندي كورديلفسكي تركيزات كبيرة من الغبار في نقاط طروادة في نظام الأرض والقمر. أكدت أداة DIRBE الموجودة على القمر الصناعي COBE ملاحظات IRAS السابقة لحلقة غبار تتبع مدار الأرض حول الشمس. ويرتبط وجود هذه الحلقة ارتباطًا وثيقًا بنقاط طروادة، لكن القصة معقدة بسبب تأثيرات الضغط الإشعاعي على حبيبات الغبار.
في عام 2010، أكد تلسكوب WISE التابع لناسا أخيرًا وجود أول كويكب طروادة (2010 TK7) حول نقطة لاغرانج الرائدة على الأرض.
لاغرانج.. صاحب المساهمات العظيمة في نظرية الأعداد والميكانيكا التحليلية والسماوية
1736- 1813/ إيطالي- فرنسي
قدم مساهمات كبيرة في مجالات التحليل ونظرية الأعداد والميكانيكا الكلاسيكية والسماوية. ويعد من أعظم العلماء في القرن السابع عشر،من أهم أعماله كتاب الميكانيكا التحليلية.
جدول المحتويات
الولادة والنشأة:
ولد جوزيبي لويجي لاغرانجيا أو جوزيبي لودوفيكو دي لاغرانج تورنييه والمعروف باسم جوزيف لويس لاغرانج بتاريخ 25 يناير عام 1736في مدينة تورينو الإيطالية.
كان لاغرانج البكر من بين أحد عشر طفلاً، وهو جوزيبي لودوفيكو لاغرانجيا، من أصل إيطالي وفرنسي. كان جده الأكبر لأبيه نقيبًا فرنسيًا في سلاح الفرسان، وتنحدر عائلته من منطقة تور الفرنسية. بعد أن خدم في عهد لويس الرابع عشر، دخل في خدمة تشارلز إيمانويل الثاني، دوق سافوي، وتزوج من كونتي من العائلة الرومانية النبيلة. كان والد لاغرانج، جوزيبي فرانشيسكو لودوفيكو، دكتوراً في القانون بجامعة تورينو، بينما كانت والدته الطفلة الوحيدة لطبيب ثري من كامبيانو، في ريف تورينو.
الدراسة:
فضٌل لاغرانج اللغة اللاتينية فدرس بكلية تورينو. وفي بدايته لم يهتم بالرياضيات ولكنه الوضع تغير كلياً عند قرأ نسخةً من عملٍ لإدمون هالي ُنشر عام 1693 يتعلق باستخدام الجبر في البصريات. اعتمد لاغرانج على التعليم الذاتي أكثر من اعتماده على الدراسة مع علماء الرياضيات.
الأعمال:
انتخب جوزيف لاغرانج عام 1756 كعضوٍ في أكاديمية برلين، فساهم بعد عام في تأسيس الأكاديمية الملكية للعلوم في تورينو التي نشرت المجلات العلمية وقد ساهم لاغرانج بشكلٍ كبيرٍ في أول ثلاثة مجلدات نشرت من قبل أكاديمية برلين ضمت هذه المجلدات الثلاث مجموعة من المواضيع المتنوعة،كما نشر عملاً قصيراً في حساب الاحتمالات بالتفاضل والتكامل، وأجرى دراسة هامةً عن انتشار الأصوات، مما أسهم إسهاماً هاماً في نظرية السلاسل المهتزة.
وفي أوراقٍ نشرها في المجلد الثالث، درس لاغرانج تكامل المعادلات التفاضلية ووسع تلك المفاهيم لتطبيقات مختلفة مثل ميكانيكا الموائع، حيث قدم الاقتران اللاغرانجي.
كما تضمن المجلد طرقاً لحل نظم المعادلات التفاضلية الخطية باستخدام التعويض الخطي وذلك لأول مرة. وبالإضافة لذلك، طبق أساليبه في دراسة مداري كوكب المشتري وزحل، تم تعيينه عام 1766 في منصب أويلر في أكاديمية برلين، فكون صداقة مع الرياضي السويسري يوهان لامبرت.
وخلال مسيرته العلمية التي استمرت عشرين عاماً نشر لاغرانج أوراق علمية عالية الجودة ،حيث تضمن عمله في برلين العديد من المواضيع: علم الفلك، استقرار النظام الشمسي، الميكانيكا، الديناميكا، ميكانيكا الموائع، الاحتمالات، وأسس حساب التفاضل والتكامل.
كما عمل على نظرية العدد، حيث أثبت في عام 1770 أن كل عدد صحيح موجب يساوي مجموع أربعة أعداد مربعة.
في عام 1770، قدم عملاً هاماً أجرى فيه تحقيقاً أساسياً في إمكانية حل معادلات من الدرجة الرابعة وأقل باستخدام الجذور، وفي 1771، أثبت نظرية ويلسون.
كما نشر ورقةً تُعتبر الأولى من نوعهاً في الإشارة إلى جذور المعادلات ككميات مجردة بدلاً من أن يكون لها قيم رقمية، كما درس لاغرانج تبادلي الجذور، وهي التي يمكن اعتبارها الخطورة الأولى في تطوير نظرية المجموعات التي طُورت من قبل روفيني، غالويس وكوشي.
بعد وفاة زوجته عام 1787ترك لاغرانج برلين وسافر إلى باريس ليكمل ما تبقى من حياته فيها، حيث أصبح عضواً في أكاديمية العلوم في باريس، وقدم خلال حياته في باريس مساهمات كبيرة في علم الميكانيكا، إلا أنه لم ينتج عملاً شاملًا.
وقد قرر أن يكتب عملاً نهائياً يتضمن مساهماته، حيث لخص في كتاب الميكانيكا التحليلية Mécanique analytique جميع الأعمال التي قيم بها في مجال الميكانيكا منذ زمن نيوتن، وقد تميز باستخدامه المعادلات التفاضلية، وبذلك فقد حول لاغرانج علم الميكانيكا إلى فرعٍ من فروع التحليل الرياضي.
وفي مايو 1790، أصبح لاغرانج عضواً في لجنة أكاديمي العلوم لتوحيد الأوزان والقياسات. حيث عملوا على تطوير النظام المتري، وفي عام 1794، تأسست مدرسة الفنون التطبيقية The Ecole Polytechnique، وكان لاغرانج أول أستاذ تحليل فيها.
وبعد عام، تأسست مدرسة المعلمين Ecole Normale بهدف تدريب معلمي المدارس، وهناك درس لاغرانج دورات في الرياضيات الابتدائية.
نشر لاغرانج مجلدين اثنين حول محاضراته في حساب التفاضل والتكامل. وفي عام 1797، نشر أول نظرية عن الاقترانات بمتغير حقيقي من خلال كتاب نظرية الدوال التحليلية Théorie des fonctions analytique.
وفي عام 1808 كرم إمبراطور فرنسا نابليون لاغرانج وأعطاه وسام جوقة الشرف. وبعد ذلك بعامين، بدأ مراجعة كتاب الميكانيكا التحليلية Mécanique analytique، لكنه لم يتمكن من إكمال سوى ثلثيه قبل وفاته.
نظرية الأعداد:
تتناول لاغرانج العديد من أوراقه المبكرة أيضًا مسائل نظرية الأعداد. وكان أول أوروبي يثبت أن معادلة بيل x2 − ny2 = 1 لها حل غير تافه في الأعداد الصحيحة لأي عدد طبيعي غير مربع n.
وأثبت النظرية التي ذكرها باشيه دون مبرر، وهي أن كل عدد صحيح موجب هو مجموع أربعة مربعات، 1770.
لقد أثبت نظرية ويلسون (لأي عدد صحيح n > 1): n هو عدد أولي إذا وفقط إذا (n – 1)! + 1 هو مضاعف لـ n، 1771.
قدمت أوراقه البحثية في الأعوام 1773 و1775 و1777 عروضًا لعدة نتائج أعلن عنها فيرما، ولم يتم إثباتها من قبل.
طوّر كتابه Recherches d’Arithmétique عام 1775 نظرية عامة عن الأشكال التربيعية الثنائية للتعامل مع المشكلة العامة المتمثلة في متى يمكن تمثيل عدد صحيح بالشكل ax2 + by2 + cxy.
وقدم مساهمات في نظرية الكسور المستمرة.
الحياة الشخصية:
تزوج لاغرانج عام 1767من قريبته فيتوريا كونتي، ولم يكن لهما أي أطفال، توفيت فيتوريا بعد صراعها مع المرض عام 1783.
وعام 1792 تزوج من ابنة الأربعة وعشرين عام رينيه فرانسوا أديلايد لو مونييه، ابنة زميله تشارلز بيير لو مونييه، استمر زواجهما إلى حين وفاته عام 1813.
الوفاة:
عانى لاغرانج من نوبات إغماء فتوفي بتاريخ 12 أبريل عام 1813 في باريس ودفن بمقبرة العظماء.
الجوائز والتكريمات:
- قبل أسبوعٍ من وفاته في باريس عام 1813، مُنح وسام الصليب الأكبر Grand Croix of the Ordre Impérial de la Réunion.
- وسام جوقة الشرف من فرنسا عام 1808.
- جائزة الأكاديمية الفرنسية للعلوم.
- تم تسمية نقاط لاغرانج على اسمه ( هي مواقع في الفضاء حيث تنتج قوى الجاذبية لنظام مكون من جسمين مثل الشمس والأرض مناطق محسنة من الجذب والتنافر).
الأقوال:
- ” إذا كنت قد ورثت ثروة، فربما لم يكن من المفترض أن ألقي نصيبي في الرياضيات”.
- ” وطالما تم الفصل بين الجبر والهندسة، كان تقدمهما بطيئًا واستخداماتهما محدودة؛ ولكن عندما اتحد هذين العلمين، فقد أعار كل منهما قوى متبادلة، وسارا معًا نحو الكمال”.
- ” لم يستغرق الأمر من الغوغاء سوى لحظة واحدة لإزالة رأسه؛ قرن لن يكفي لإعادة إنتاجه”.
- “لقد كان نيوتن أعظم عبقري وجد على الإطلاق، وأكثرهم حظًا، لأننا لا نستطيع أن نجد أكثر من مرة نظامًا للعالم يجب تأسيسه”.
- ” لقد اعتبرت قراءة الأطروحات الكبيرة للتحليل الخالص أمرًا عديم الفائدة تمامًا: حيث يمر عدد كبير جدًا من الأساليب مرة واحدة أمام أعيننا. في الأعمال التطبيقية يجب على المرء أن يدرسها؛ يحكم المرء على فائدتها هناك ويقيم طريقة الاستفادة منها”.
- ” العمليات العادية للجبر تكفي لحل المشاكل في نظرية المنحنيات”.
المصادر:
- https://science.nasa.gov/
- https://www.ibelieveinsci.com/
- https://en.wikipedia.org/
- https://www.azquotes.com/
- https://mathshistory.st-andrews.ac.uk/
لاغرانج.. صاحب المساهمات العظيمة في نظرية الأعداد والميكانيكا التحليلية والسماوية
حقائق سريعة
- ميكانيك لاغرانج هي إعادة صياغة للميكانيك الكلاسيكية (ميكانيك نيوتن)، قام لاغرانج عام 1788. في الميكانيك اللاغرانجية: يُحسب مسار جسم ما من خلال حل معادلة لاغرانج بأحد شكليها اللذين يختلفان عن بعضهما بكيفية التعامل مع التقييدات الفيزيائية ( التقييدات في الفيزياء هي أمور لا يمكن للنظام الفيزيائي تجاوزها).
- عام 1787، عندما كان عمره 51 عامًا، انتقل من برلين إلى باريس وأصبح عضوًا في الأكاديمية الفرنسية للعلوم. وبقي في فرنسا حتى نهاية حياته. كان له دور فعال في عملية التقسيم العشري في فرنسا الثورية، وأصبح أول أستاذ للتحليل في مدرسة البوليتكنيك عند افتتاحها في عام 1794، وكان عضوًا مؤسسًا في مكتب خطوط الطول، وأصبح عضوًا في مجلس الشيوخ في عام 1799.
- كان من المفترض أن يحافظ والده، الذي كان مسؤولاً عن الصندوق العسكري للملك وكان أمين صندوق مكتب الأشغال العامة والتحصينات في تورينو، على وضع اجتماعي جيد وثروة، ولكن قبل أن يكبر ابنه كان قد فقد معظم ممتلكاته في المضاربات.
- اخترع لاغرانج طريقة حل المعادلات التفاضلية المعروفة باسم اختلاف المعلمات.
معلومات نادرة
- لماذا غير اسمه؟ عندما ولد، كانت تورينو قد تحولت بالفعل إلى عاصمة سردينيا. قام لاغرانج فيما بعد بتغيير اسمه ليبدو فرنسيًا أكثر عندما أصبح مواطنًا متجنسًا في بلده.
- ما هي نقطة لاغرانج؟
نقاط لاغرانج هي مواضع في الفضاء حيث تميل الأجسام المرسلة إلى البقاء في مكانها. عند نقاط لاغرانج، فإن قوة الجاذبية لكتلتين كبيرتين تساوي بدقة قوة الجذب المركزي اللازمة لجسم صغير ليتحرك معهم. يمكن للمركبات الفضائية استخدام هذه النقاط في الفضاء لتقليل استهلاك الوقود اللازم للبقاء في موضعها.
نقاط لاغرانج هي مواقع في الفضاء حيث تنتج قوى الجاذبية لنظام مكون من جسمين مثل الشمس والأرض مناطق محسنة من الجذب والتنافر. يمكن استخدامها بواسطة المركبات الفضائية لتقليل استهلاك الوقود اللازم للبقاء في الموقع.
تم تسمية نقاط لاغرانج على اسم عالم الرياضيات الإيطالي الفرنسي جوزيفي لويس لاغرانج.
هناك خمس نقاط خاصة حيث يمكن للكتلة الصغيرة أن تدور بنمط ثابت مع كتلتين أكبر. نقاط لاغرانج هي مواضع حيث قوة الجاذبية لكتلتين كبيرتين تساوي بدقة قوة الجذب المركزي المطلوبة لجسم صغير ليتحرك معهم. هذه المشكلة الرياضية، المعروفة باسم “مشكلة الأجسام الثلاثة العامة”، تناولها لاغرانج في بحثه الحائز على جائزة (Essai sur le Problème des Trois Corps، 1772).
من بين نقاط لاغرانج الخمس، هناك ثلاث نقاط غير مستقرة واثنتان مستقرتان. تقع نقاط لاغرانج غير المستقرة – المسماة L1 وL2 وL3 – على طول الخط الذي يربط بين الكتلتين الكبيرتين. تشكل نقاط لاغرانج المستقرة – المسماة L4 وL5 – قمة مثلثين متساويين الأضلاع لهما كتل كبيرة في رؤوسهما. يقود L4 مدار الأرض ويتبعه L5
توفر النقطة L1 لنظام الأرض والشمس رؤية متواصلة للشمس وهي حاليًا موطن للقمر الصناعي للمرصد الشمسي والغلاف الشمسي SOHO.
كانت النقطة L2 في نظام الأرض والشمس موطنًا للمركبة الفضائية WMAP، والموطن الحالي لبلانك، والموطن المستقبلي لتلسكوب جيمس ويب الفضائي. يعتبر L2 مثاليًا لعلم الفلك لأن المركبة الفضائية قريبة بما يكفي للتواصل بسهولة مع الأرض، ويمكنها إبقاء الشمس والأرض والقمر خلف المركبة الفضائية للحصول على الطاقة الشمسية و(مع التدريع المناسب) توفر رؤية واضحة للفضاء السحيق لتلسكوباتنا. النقطتان L1 وL2 غير مستقرتين على نطاق زمني يبلغ حوالي 23 يومًا، الأمر الذي يتطلب من الأقمار الصناعية التي تدور حول هذه المواقع أن تخضع لتصحيحات منتظمة للمسار والارتفاع.
ومن غير المرجح أن تجد ناسا أي فائدة للنقطة L3 لأنها تظل مخفية خلف الشمس في جميع الأوقات. كانت فكرة الكوكب المخفي موضوعًا شائعًا في كتابة الخيال العلمي.
تعد النقطتان L4 وL5 موطنًا لمدارات مستقرة طالما أن نسبة الكتلة بين الكتلتين الكبيرتين تتجاوز 24.96. يتم استيفاء هذا الشرط لكل من نظامي الأرض والشمس والأرض والقمر، وللعديد من أزواج الأجسام الأخرى في النظام الشمسي. غالبًا ما تسمى الأجسام التي تدور حول النقطتين L4 وL5 بأحصنة طروادة نسبة إلى الكويكبات الثلاثة الكبيرة أجاممنون وأخيل وهيكتور التي تدور في النقطتين L4 وL5 من نظام المشتري والشمس. (بحسب هوميروس، كان هيكتور بطل طروادة الذي قُتل على يد أخيل أثناء حصار الملك أجاممنون لطروادة). هناك المئات من كويكبات طروادة في النظام الشمسي. معظمها يدور حول كوكب المشتري، لكن البعض الآخر يدور حول المريخ. بالإضافة إلى ذلك، فإن العديد من أقمار زحل لها أقمار طروادة مرافقة.
في عام 1956، اكتشف عالم الفلك البولندي كورديلفسكي تركيزات كبيرة من الغبار في نقاط طروادة في نظام الأرض والقمر. أكدت أداة DIRBE الموجودة على القمر الصناعي COBE ملاحظات IRAS السابقة لحلقة غبار تتبع مدار الأرض حول الشمس. ويرتبط وجود هذه الحلقة ارتباطًا وثيقًا بنقاط طروادة، لكن القصة معقدة بسبب تأثيرات الضغط الإشعاعي على حبيبات الغبار.
في عام 2010، أكد تلسكوب WISE التابع لناسا أخيرًا وجود أول كويكب طروادة (2010 TK7) حول نقطة لاغرانج الرائدة على الأرض.